Pada sumbu x berlaku persamaan gerak lurus beraturan.
Al-Quran Surat At-Taubah ayat 129
Jika mereka berpaling (dari keimanan), maka katakanlah: "Cukuplah Allah bagiku; tidak ada Tuhan selain Dia. Hanya kepada-Nya aku bertawakkal dan Dia adalah Tuhan yang memiliki 'Arsy yang agung.

Al-Quran Surat Al-Kahfi 110
Katakanlah: Sesungguhnya aku ini manusia biasa seperti kamu, yang diwahyukan kepadaku: "Bahwa sesungguhnya Tuhan kamu itu adalah Tuhan yang Esa." Barangsiapa mengharap perjumpaan dengan Tuhannya, maka hendaklah ia mengerjakan amal yang saleh dan janganlah ia mempersekutukan seorangpun dalam beribadat kepada Tuhannya.

Al-Quran Surat Al-Israa’ 107
Katakanlah: "Berimanlah kamu kepadanya atau tidak usah beriman (sama saja bagi Allah). Sesungguhnya orang-orang yang diberi pengetahuan sebelumnya apabila Al Quran dibacakan kepada mereka, mereka menyungkur atas muka mereka sambil bersujud,

Al-Quran Surat Al-Israa’ 111
Dan katakanlah: "Segala puji bagi Allah Yang tidak mempunyai anak dan tidak mempunyai sekutu dalam kerajaan-Nya dan Dia bukan pula hina yang memerlukan penolong dan agungkanlah Dia dengan pengagungan yang sebesar-besarnya.

Al-Quran Surat Al-Furqon 2
yang kepunyaan-Nya-lah kerajaan langit dan bumi, dan Dia tidak mempunyai anak, dan tidak ada sekutu bagiNya dalam kekuasaan(Nya), dan dia telah menciptakan segala sesuatu, dan Dia menetapkan ukuran-ukurannya dengan serapi-rapinya.

Al-Quran Surat An-Nuur 64
Ketahuilah sesungguhnya kepunyaan Allahlah apa yang di langit dan di bumi. Sesungguhnya Dia mengetahui keadaan yang kamu berada di dalamnya (sekarang). Dan (mengetahui pula) hati (manusia) dikembalikan kepada-Nya, lalu diterangkan-Nya kepada mereka apa yang telah mereka kerjakan. Dan Allah Maha mengehui segala sesuatu.

Al-Quran Surat Al-Qashash 88
Janganlah kamu sembah di samping (menyembah) Allah, tuhan apapun yang lain. Tidak ada Tuhan (yang berhak disembah) melainkan Dia. Tiap-tiap sesuatu pasti binasa, kecuali Allah. Bagi-Nyalah segala penentuan, dan hanya kepada-Nyalah kamu dikembalikan.

Al-Quran Surat Luqman 34
Sesungguhnya Allah, hanya pada sisi-Nya sajalah pengetahuan tentang Hari Kiamat; dan Dia-lah Yang menurunkan hujan, dan mengetahui apa yang ada dalam rahim. Dan tiada seorangpun yang dapat mengetahui (dengan pasti) apa yang akan diusahakannya besok[1187]. Dan tiada seorangpun yang dapat mengetahui di bumi mana dia akan mati. Sesungguhnya Allah Maha Mengetahui lagi Maha Mengenal.

31 Mei 2016
Gerak Parabola
Pada sumbu x berlaku persamaan gerak lurus beraturan.
Kecepatan sudut
w ̅= kecepatan sudut rata-rata (rad/s)
∆θ = Perpindahan sudut (rad)
∆t = selang waktu (s)
Perpindahan sudut
 Perpindahan sudut adalah perpindahan partikel pada gerak melingkar. Perhatikan posisi roda pada gambar disamping. Untuk berpindah dari posisi a ke b, roda telah menempuh perpindahan sudut θ. Roda telah berputar sejauh θ ketika sebuah titik pada pinggiran roda telah bergerak melalui jarak linear gerak s. Satuan θ dalam SI adalah radian. Nilai θ dalam radian (rad) adalah perbandingan antara jarak linear s dengan jari-jari roda r.
Perpindahan sudut adalah perpindahan partikel pada gerak melingkar. Perhatikan posisi roda pada gambar disamping. Untuk berpindah dari posisi a ke b, roda telah menempuh perpindahan sudut θ. Roda telah berputar sejauh θ ketika sebuah titik pada pinggiran roda telah bergerak melalui jarak linear gerak s. Satuan θ dalam SI adalah radian. Nilai θ dalam radian (rad) adalah perbandingan antara jarak linear s dengan jari-jari roda r.S = jarak linear (m)
R = jarak partikel ke pusat lingkaran (m)
1 putaran = 3600 =2 π rad
1 rad = 180/ π derajat = 57,30
30 Mei 2016
Gerak Melingkar Berubah Beraturan (GMBB)
_1.jpg)
_2.jpg)
_3.jpg)
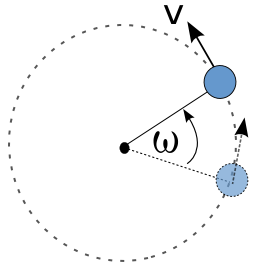
Gerak Melingkar Beraturan
Besaran-besaran dalam Gerak Melingkar Beraturan
Periode (T) didefinisikan sebagai selang waktu yang dipergunakan oleh suatu titik materi pada benda yang berputar terhadap suatu proses tertentu, untuk menempuh satu kali putaran (satu kali melingkar). Frekuensi (f) didefinisikan sebagai banyaknya putaran yang dapat dilakukan oleh suatu titik materi yang berputar terhadap suatu proses tertentu, dalam selang waktu satu sekon.
Secara matematis, periode, dan frekuensi dirumuskan sebagai berikut:
n= banyaknya putaran
t= waktu tempuh (s)
T= periode(s)
f= frekuensi (Hz)
Kecepatan linear (v) adalah hasil bagi panjang lintasan linear yang ditempuh partikel dengan selang waktu tempuhnya. Sedangkan kecepatan sudut (ω) adalah hasil bagi sudut pusat yang ditempuh partikel dengan selang waktunya.
Secara matematis, kecepatan linear dan kecepatan sudut dirumuskan sebagai berikut
Pada partikel yang melakukan gerak melingkar beraturan, percepatan tangensial bernilai nol tetapi partikel tersebut masih mengalami percepatan sentripetal αs. Percepatan sentripetal didefinisikan sebagai percepatan yang selalu tegak lurus terhadap kecepatan linearnya dan mengarah ke pusat lingkaran.
Percepatan sentripetal dapat dicarai dengan persamaan beriku
Analogi dari gerak beraturan adalah gerak melingkar beraturan. Oleh karena itu, persamaan untuk gerak melingkar beraturan mirip dengan gerak lurus beraturan. Dalam GMB, kecepatan sudut rata-rata sema dengan kecepatan sudut sesaat.
Gerak Vertikal Ke Atas
 Gerak vertikal merupakan gerakan benda arah vertikal dengan kecepatan awal (Vo = 0). Gerak vertikal ini dibedakan mejadi dua, yaitu gerak vertikal ke atas dan gerak vertikal ke bawah
Gerak vertikal merupakan gerakan benda arah vertikal dengan kecepatan awal (Vo = 0). Gerak vertikal ini dibedakan mejadi dua, yaitu gerak vertikal ke atas dan gerak vertikal ke bawah
Gerak Jatuh Bebas



Gerak Lurus Berubah Beraturan
 Coba kamu perhatikan apabila sebuah sepeda motor bergerak menuruni sebuah bukit, bagaimanakah kecepatannya? Tentu saja kecepatannya semakin bertambah besar. Gerak lurus berubah beraturan (GLBB) adalah gerak benda pada lintasan lurus dengan kecepatannya berubah secara teratur tiap detik. Kamu tentunya masih ingat bahwa perubahan kecepatan tiap detik adalah percepatan. Dengan demikian, pada GLBB benda mengalami percepatan secara teratur atau tetap. Hubungan antara besar kecepatan (v) dengan waktu (t) pada gerak lurus berubah beraturan (GLBB) ditunjukkan pada grafik di bawah ini.
Coba kamu perhatikan apabila sebuah sepeda motor bergerak menuruni sebuah bukit, bagaimanakah kecepatannya? Tentu saja kecepatannya semakin bertambah besar. Gerak lurus berubah beraturan (GLBB) adalah gerak benda pada lintasan lurus dengan kecepatannya berubah secara teratur tiap detik. Kamu tentunya masih ingat bahwa perubahan kecepatan tiap detik adalah percepatan. Dengan demikian, pada GLBB benda mengalami percepatan secara teratur atau tetap. Hubungan antara besar kecepatan (v) dengan waktu (t) pada gerak lurus berubah beraturan (GLBB) ditunjukkan pada grafik di bawah ini.Gerak Lurus Beraturan (GLB)
 Pernahkah kamu mengamati bagaimana jalannya kereta api? Lintasannya lurus, parabola atau lingkaran? Gerak suatu benda dalam lintasan lurus disebut gerak lurus. Buah kelapa yang jatuh dari pohonnya adalah contoh gerak lurus. Gerak bumi mengelilingi matahari merupakan gerak dengan kecepatan tetap dengan waktu tempuh satu tahun. Menurut bentuk lintasannya, gerak lurus dibagi menjadi gerak lurus beraturan dan gerak lurus berubah beraturan.
Pernahkah kamu mengamati bagaimana jalannya kereta api? Lintasannya lurus, parabola atau lingkaran? Gerak suatu benda dalam lintasan lurus disebut gerak lurus. Buah kelapa yang jatuh dari pohonnya adalah contoh gerak lurus. Gerak bumi mengelilingi matahari merupakan gerak dengan kecepatan tetap dengan waktu tempuh satu tahun. Menurut bentuk lintasannya, gerak lurus dibagi menjadi gerak lurus beraturan dan gerak lurus berubah beraturan.Percepatan
 Suatu benda akan mengalami percepatan apabila benda tersebut bergerak dengan kecepatan yang tidak konstan dalam selang waktu tertentu. Misalnya, ada sepeda yang bergerak menuruni sebuah bukit memiliki suatu kecepatan yang semakin lama semakin bertambah selama geraknya. Gerak sepeda tersebut dikatakan dipercepat. Jadi percepatan adalah kecepatan tiap satuan waktu. Secara matematis dapat ditulis sebagai berikut.
Suatu benda akan mengalami percepatan apabila benda tersebut bergerak dengan kecepatan yang tidak konstan dalam selang waktu tertentu. Misalnya, ada sepeda yang bergerak menuruni sebuah bukit memiliki suatu kecepatan yang semakin lama semakin bertambah selama geraknya. Gerak sepeda tersebut dikatakan dipercepat. Jadi percepatan adalah kecepatan tiap satuan waktu. Secara matematis dapat ditulis sebagai berikut.Kecepatan dan Kelajuan
Kecepatan Rata-Rata dan Kelajuan Rata-Rata
Kelajuan rata-rata merupakan jarak yang ditempuh tiap satuan waktu. Secara matematis dapat dituliskan sebagai berikut
Jarak dan Perpindahan
Suatu benda dikatakan bergerak jika benda itu mengalami perubahan kedudukan terhadap titik tertentu sebagai acuan. Jadi, gerak adalah perubahan posisi atau kedudukan terhadap titik acuan tertentu. Gerak juga dapat dikatakan sebagai perubahan kedudukan suatu benda dalam selang waktu tertentu. Berbeda halnya dengan peristiwa berikut, orang berlari di mesin lari fitnes (mesin kebugaran), anak yang bermain komputer dan lain sebagainya. Apakah mereka mengalami perubahan posisi atau kedudukan dalam selang waktu tertentu?
Kegiatan tersebut tidak mengalami perubahan posisi atau kedudukan karena kerangka acuannya diam. Penempatan kerangka acuan dalam peninjauan gerak merupakan hal yang sangat penting, mengingat gerak dan diam itu mengandung pengertian yang relatif. Sebagai contoh, ada seorang yang duduk di dalam kereta api yang sedang bergerak, dapat dikatakan bahwa orang tersebut diam terhadap kursi yang didudukinya dan terhadap kereta api tersebut, namun orang tersebut bergerak relatif terhadap stasiun maupun terhadap pohon-pohon yang dilewatinya.
Jarak dan Perpindahan
Contoh lain, ada seorang pejalan kaki bergerak ke utara sejauh 3 km, kemudian berbelok ke timur sejauh 4 km, lalu berhenti. Berapa jarak yang ditempuh siswa tersebut? Berapa pula perpindahannya?
Dengan demikian, jarak didefinisikan sebagai panjang seluruh lintasan yang ditempuh. Perpindahan merupakan jarak dan arah dari kedudukan awal ke kedudukan akhir atau selisih kedudukan akhir dengan kedudukan awal. Jarak merupakan besaran skalar, sedangkan perpindahan merupakan besaran vektor.
Besaran Vektor
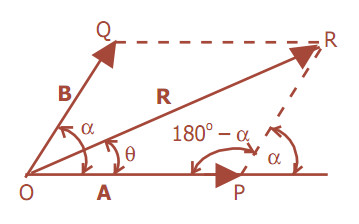
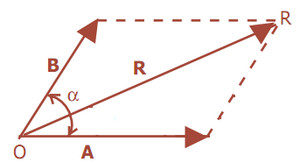
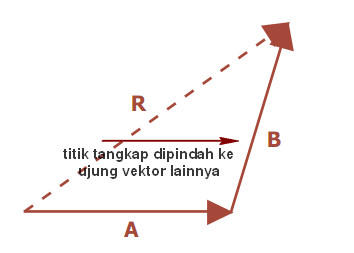
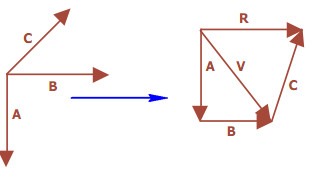
Vektor pada bidang datar mempunyai 2 komponen yaitu pada sumbu x dan sumbu y. Khusus untuk vektor yang segaris dengan sumbu x atau y berarti hanya mempunyai 1 komponen. Komponen vektor adalah vektor yang bekerja menuyusun suatu vektor hasil (resultan vektor). Oleh karenanya vektor bisa dipindahkan titik pangkalnya asalkan tidak berubah besar dan arahnya.
Inti dari operasi penjumlahan vektor ialah mencari sebuah vektor yang komponen-komponennya adalah jumlah dari kedua komponen-komponen vektor pembentuknya atau secara sederhana berarti mencari resultan dari 2 vektor. Aga susah memang dipahami dari definisi tertulis. Kita coba memahaminya dengan contoh.
(OR)2 = (OP)2 + (PR)2 - 2(OP)(PR) cos (-cos α)
(OR)2 = (OP)2 + (PR)2 - 2(OP)(PR) cos α
Jika OP = A, PR = B, dan Resultan ‘R’ = OR
R2 = A2 + B2 - 2AB cos α
R = 82 + 62 + 2.6.8.cos 30
R = 64 + 36 + 96 0,5 √3
R = 100 + 48√3










 09.17.00
09.17.00
 mhharismansur
mhharismansur
















_1.jpg)
_2.jpg)
_3.jpg)
_4.jpg)
_5.jpg)
_6.jpg)
_7.jpg)